Trigonometry: Pitch of Roof
The pitch of a roof is equivalent to the hypotenuse of a triangle. The 11/18 in an 11/18 pitch, is the slope of the pitch, and we know that the slope is the rise of the run. With the knowledge that the slope is rise/run, we can deduce that the two legs are 11 and 18, with 11 being the rise and 18 being the run. Then from there, it is quite simple to find the angle of elevation. To find the angle of elevation you first set up the tangent equation: Tan A=11/18. Then you multiply each side by the inverse tangent: A= tan^-1 (11/18). Then you will get that the angle A is equal to 31 degrees.
Next, we had to find the "rafter line" if the full length of the "run" is 22ft. This was pretty easy to figure out, first, I had to set up the equation: Cos31=11/x. I chose to use the Cos equation because we were trying to find the length of the rafter which is equivalent to the hypotenuse of a triangle, and we were given the adjacent leg. Next, we simply solved the equation: x=Cos31(11), x=9.4ft.
Next, we had to find the "rafter line" if the full length of the "run" is 22ft. This was pretty easy to figure out, first, I had to set up the equation: Cos31=11/x. I chose to use the Cos equation because we were trying to find the length of the rafter which is equivalent to the hypotenuse of a triangle, and we were given the adjacent leg. Next, we simply solved the equation: x=Cos31(11), x=9.4ft.
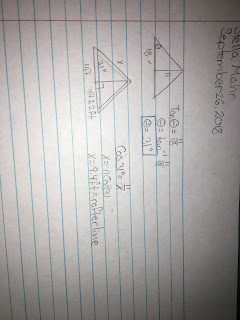
Comments
Post a Comment